Can we get causality/time-ordering from observational data
that doesn’t have time stamps?

Refresher on Bayesian networks

Bayesian networks are just visual representations of independencies.

\(P(x_1, ..., x_n)=\prod_i P(x_i|pa(x_i))\)

in this case:

\(P(A, B, C, D, E)=P(A)P(B|A)P(C|B)P(D|B)P(E|A,C)\)

Do the arrows indicate causality?

No.

These two imply the same factorization

So: meaningless arrows for now

With 3 nodes, it’s also not guaranteed.

But with a collider we can!

implied factorization: \(P(A, B, C) = P(C|A, B)P(A)P(B)\)

so: \(P(A|B)=P(A)\)

so: \(A\perp B\)

(but: \(A\not\perp C\quad B\not\perp C\quad A\not\perp C|B\quad B\not\perp C|A\quad A\not\perp B|C\))

There are 25 possible DAGs with 3 nodes

wanted: \(A\perp B\) (and no other independence)

wanted: \(A\perp B\) (and no other independence)

So, in some cases we can recover the DAG structure

Do the arrows in colliders represent causality?

Potentially.

But maybe 3 nodes is not enough to define time.

We need 4 nodes

\(A\perp B\)

\(X\perp Y|A,B\)

(there are 543 DAGs with 4 nodes...)

Try it out with this Markov chain process

\(G_t = \alpha G_{t-1} + \beta H_{t-1} + \xi_t\)

\(H_t = \gamma G_{t-1} + \delta H_{t-1} + \eta_t\)

\(\xi_t\), \(\eta_t\): iid noise (very important)

You will be able to uniquely recover the structure of the chain.

Claim:

if you have variables \(A\), \(B\), \(X\), and \(Y\) that are consistent with this DAG,

then \(A\) and \(B\) happened before \(X\) and \(Y\):

\(A, B <_T X, Y\)

(this is Statistical Time)

How can we make such a bold claim?

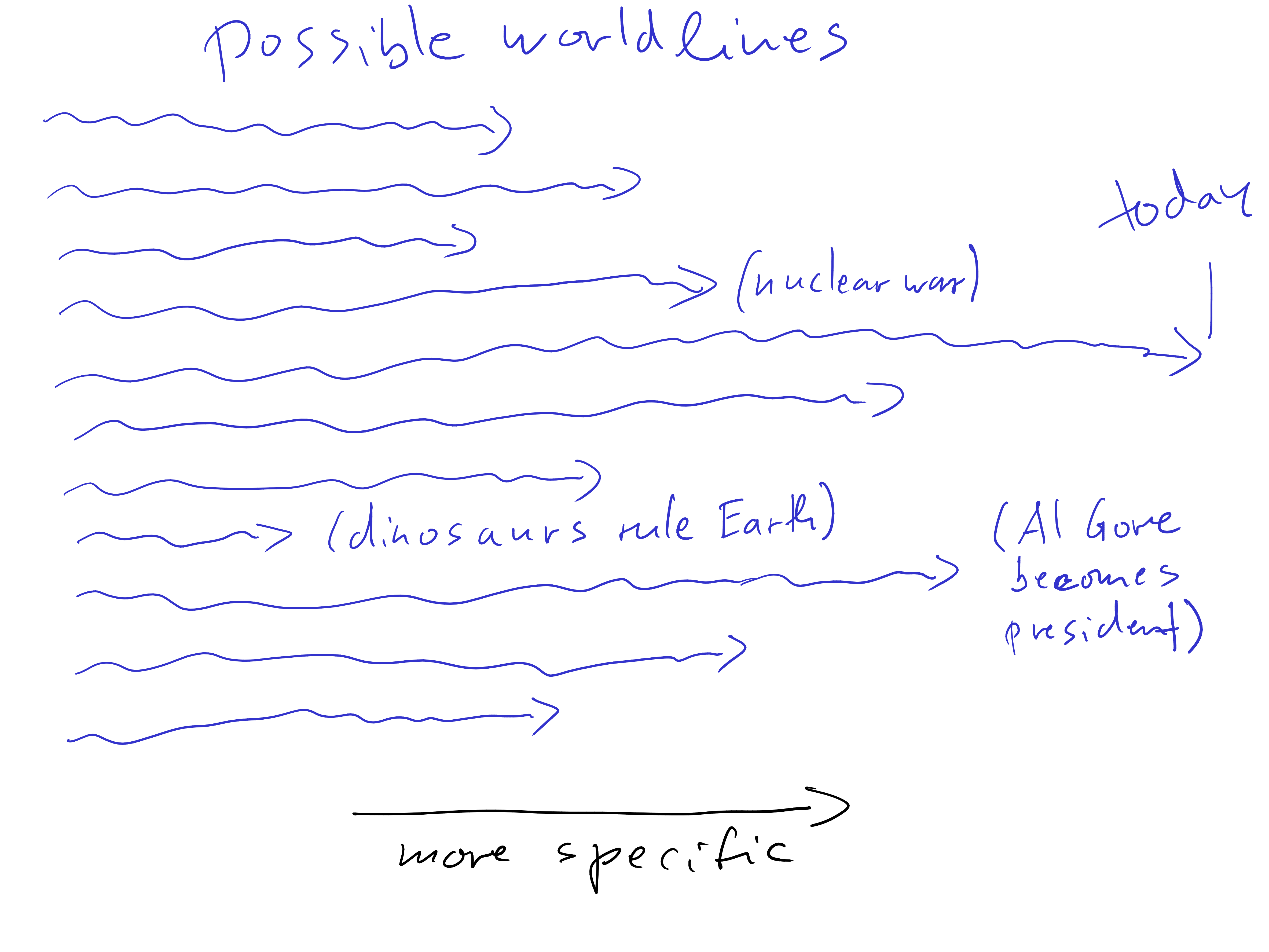
• Another insight is that things become more entangled as time goes on.
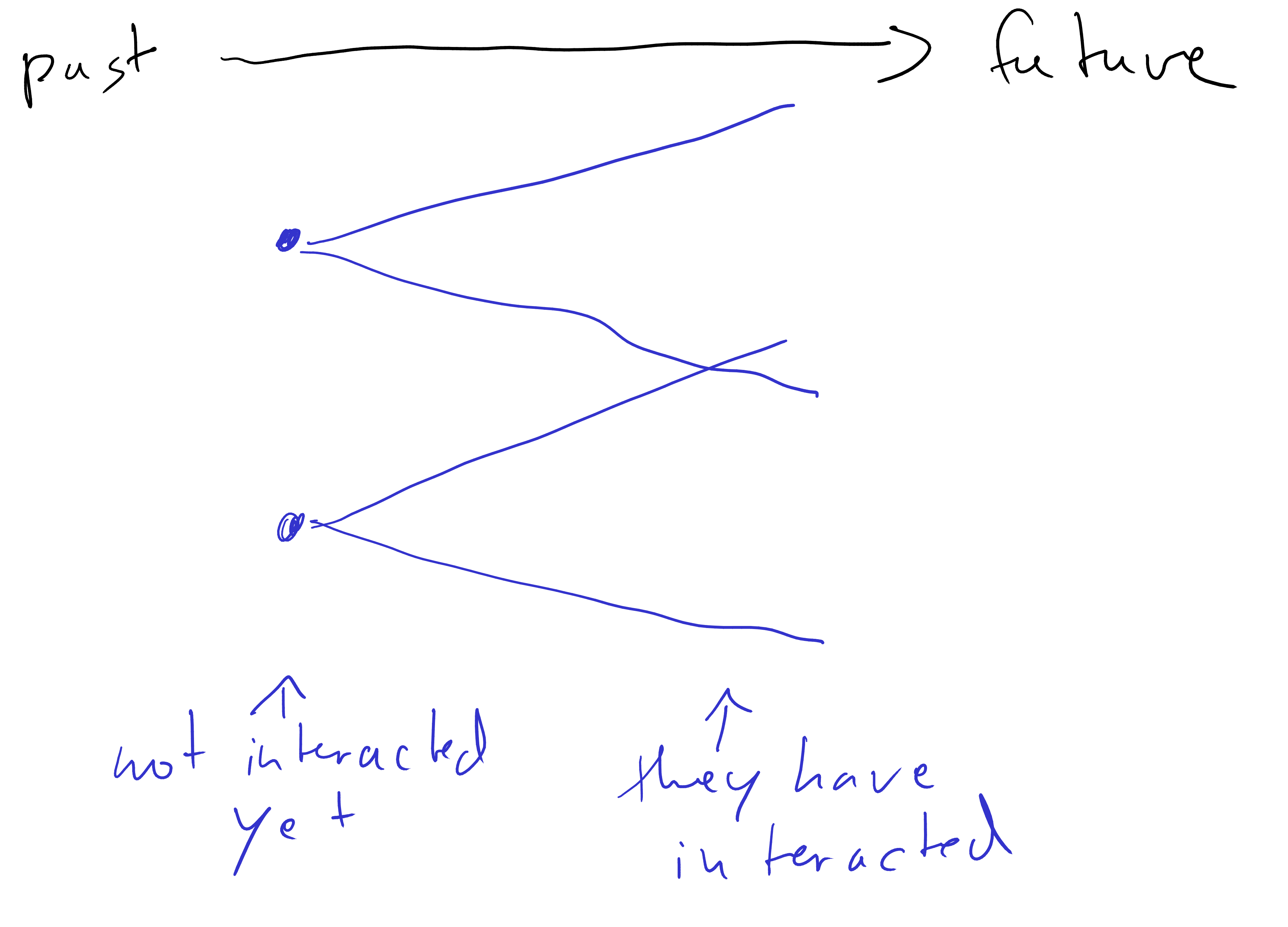
• In the past, there might be points that have not causally interacted yet.
  • But this gets rarer and rarer as time goes on.

\(X\perp Y|A,B\)

\(A\not\perp B|X,Y\)

• from the perspective of the past, the future hasn’t become entangled yet
• from the perspective of the future, the past is very entangled

Examples

of the form:

we know the true time and check whether statistical time agrees with it

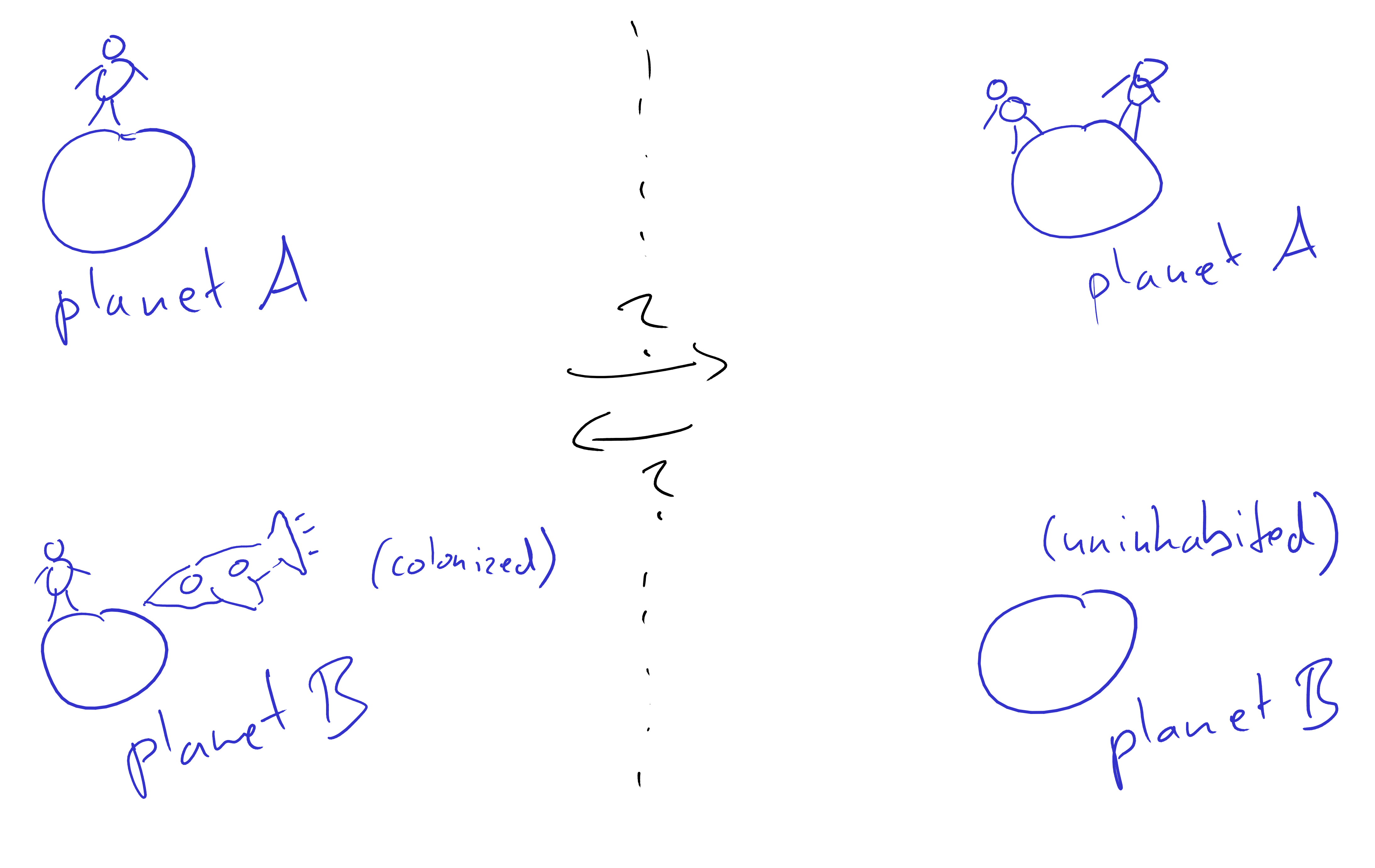
• \(A\): was there an earthquake?
• \(B\): did a burglar come to my house?
• \(X\): is the backyard window broken?
• \(Y\): is the dog in the front yard barking? (who cannot hear or see the backyard window)

\(A\perp B\) ?

\(A\not\perp B|X,Y\) ?

\(X\perp Y|A,B\) ?

\(X\not\perp Y\) ?

End